図1のブレースの軸力Nを求めてみましょう。さらに,各部材の応力も求めてください。ただし,記入していない部分は,左右,上下など同じ部材とします。
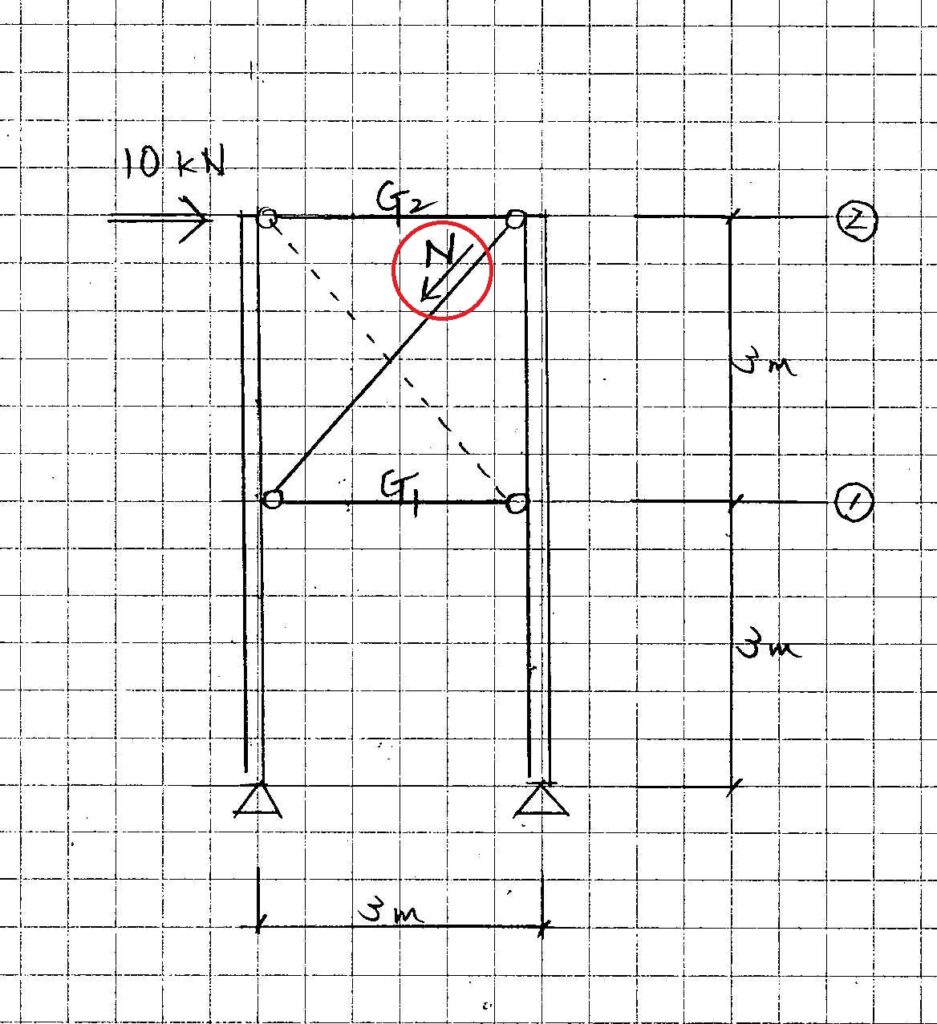
直観的にわかるやさしい問題ですが,すぐ正解を出したでしょうか。10√2[kN]としたらそれは間違いです。もう一度,図1をよく見直して下さい。この「下抜けブレース」は,私が実際に屋外階段の設計で直面し,危うく誤るところでした。
架構が対称で,応力状態が逆対称形になるので,静定構造のように,反力が力のつり合いだけによって定まります。解の数値はいちいち説明するまでもありませんが,反力R1, R2, 柱脚の剪断力,柱のM, 柱頭の剪断力(-5です),柱中央の集中荷重G1とG2の軸力などが順次求められます。
この応力図5(解答)を見ますと,柱が上部で「逆剪断」の状態になっていることがわかりますが,その分〔(-5[kN])+(-5[kN]) = -10[kN] 〕だけブレースの軸力が見かけの軸力10√2より大きくなっています。
このような応力はフィーレンディール架構にも現われ,外力よりも大きなせん断力負担になることがあるので注意を要します。
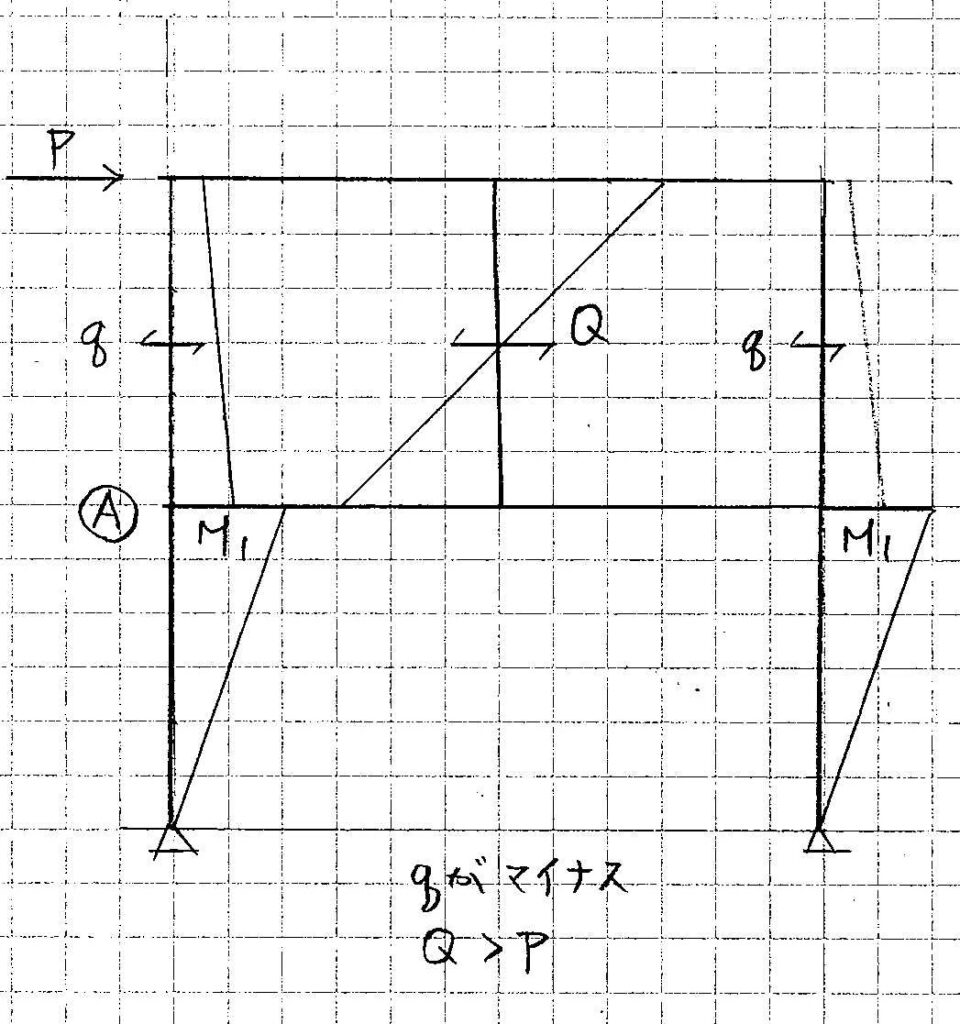
図2のように, 2階の左右の柱が「逆せん断」になることがありますが,節点Ⓐにおいて, 1階柱頭のMが大きいため,あるいは節点Ⓐに連結するはりの剛性が小さいため,上下2つの柱の曲げをまかない切れない(回転角が大きくなる)ためなどの理由から生じます。
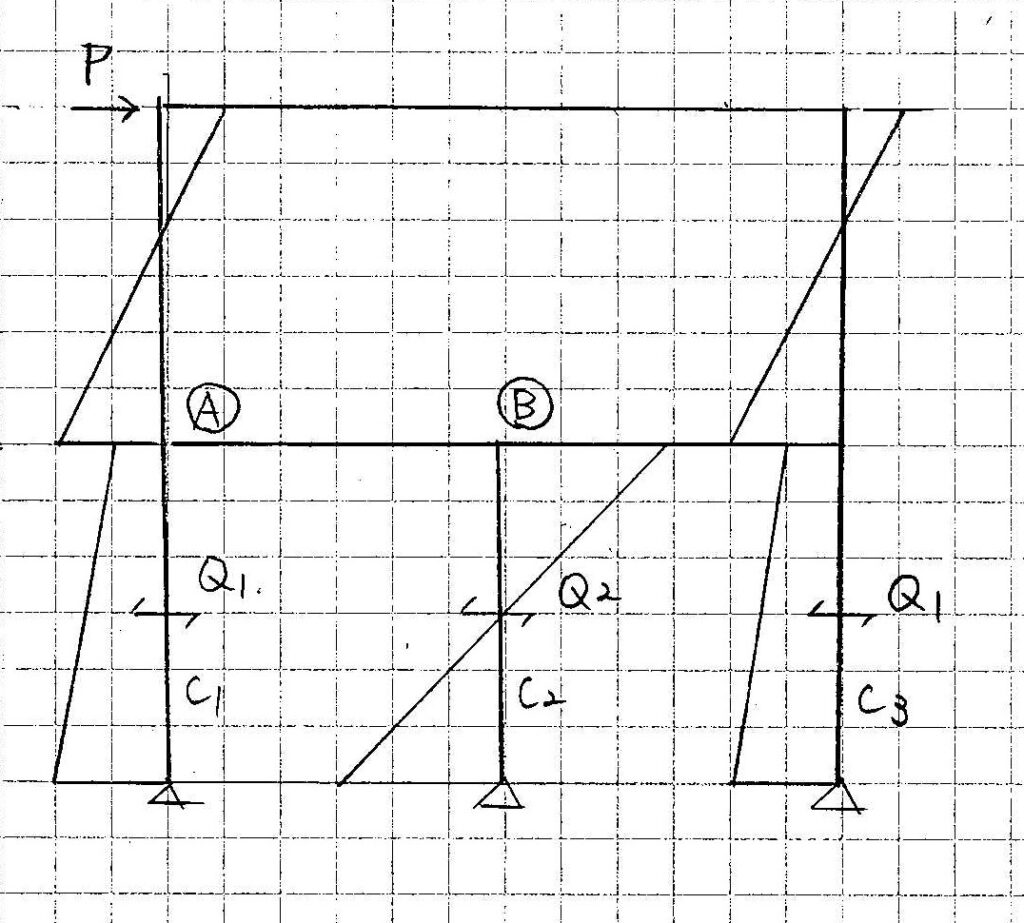
また,図3のような「2階柱ぬけ架構」でも同様なことがいえます。中柱C2の負担せん断力は, D値法による分担係数以上の値をとります。「節点ⒶにおいてC1は,上階の柱の曲げをしょい込んでいるのに比べて,節点ⒷではC2の曲げだけ面倒みればよいので余裕がある」といったところです。
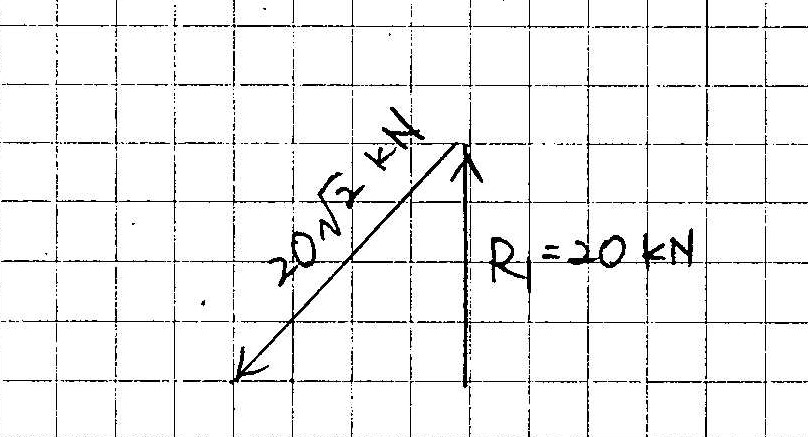
この問題は,ブレースの軸力だけを求めるなら, もっとスマートに解くことができます。中間部材G1, G2, ブレースのうち,上下方向に抵抗できるのはブレースのみだから, R1=20[kN]はブレースとのみつり合います。(図4)
【解答】
反力:R1=10[kN]x6[m]/3[m]=20[kN]
剪断力:R2=10[kN]/2=5[kN]
柱頭曲げモーメント:M1=5[kN]x3[m]=15[kN・m]
柱頭剪断力:Q2=15[kN・m]/3[m]=5[kN]

この問題を容易に解けて,まだ構造設計一級建築士でない方は,是非とも構造設計一級建築士の資格を取得してください。



コメント